Alexander Soen
Australian National University
A Connection Between Learning to Reject and Bhattacharyya Divergences
May 08, 2025Abstract:Learning to reject provide a learning paradigm which allows for our models to abstain from making predictions. One way to learn the rejector is to learn an ideal marginal distribution (w.r.t. the input domain) - which characterizes a hypothetical best marginal distribution - and compares it to the true marginal distribution via a density ratio. In this paper, we consider learning a joint ideal distribution over both inputs and labels; and develop a link between rejection and thresholding different statistical divergences. We further find that when one considers a variant of the log-loss, the rejector obtained by considering the joint ideal distribution corresponds to the thresholding of the skewed Bhattacharyya divergence between class-probabilities. This is in contrast to the marginal case - that is equivalent to a typical characterization of optimal rejection, Chow's Rule - which corresponds to a thresholding of the Kullback-Leibler divergence. In general, we find that rejecting via a Bhattacharyya divergence is less aggressive than Chow's Rule.
Domain Adaptation and Entanglement: an Optimal Transport Perspective
Mar 11, 2025Abstract:Current machine learning systems are brittle in the face of distribution shifts (DS), where the target distribution that the system is tested on differs from the source distribution used to train the system. This problem of robustness to DS has been studied extensively in the field of domain adaptation. For deep neural networks, a popular framework for unsupervised domain adaptation (UDA) is domain matching, in which algorithms try to align the marginal distributions in the feature or output space. The current theoretical understanding of these methods, however, is limited and existing theoretical results are not precise enough to characterize their performance in practice. In this paper, we derive new bounds based on optimal transport that analyze the UDA problem. Our new bounds include a term which we dub as \emph{entanglement}, consisting of an expectation of Wasserstein distance between conditionals with respect to changing data distributions. Analysis of the entanglement term provides a novel perspective on the unoptimizable aspects of UDA. In various experiments with multiple models across several DS scenarios, we show that this term can be used to explain the varying performance of UDA algorithms.
pyBregMan: A Python library for Bregman Manifolds
Aug 08, 2024Abstract:A Bregman manifold is a synonym for a dually flat space in information geometry which admits as a canonical divergence a Bregman divergence. Bregman manifolds are induced by smooth strictly convex functions like the cumulant or partition functions of regular exponential families, the negative entropy of mixture families, or the characteristic functions of regular cones just to list a few such convex Bregman generators. We describe the design of pyBregMan, a library which implements generic operations on Bregman manifolds and instantiate several common Bregman manifolds used in information sciences. At the core of the library is the notion of Legendre-Fenchel duality inducing a canonical pair of dual potential functions and dual Bregman divergences. The library also implements the Fisher-Rao manifolds of categorical/multinomial distributions and multivariate normal distributions. To demonstrate the use of the pyBregMan kernel manipulating those Bregman and Fisher-Rao manifolds, the library also provides several core algorithms for various applications in statistics, machine learning, information fusion, and so on.
Rejection via Learning Density Ratios
May 29, 2024



Abstract:Classification with rejection emerges as a learning paradigm which allows models to abstain from making predictions. The predominant approach is to alter the supervised learning pipeline by augmenting typical loss functions, letting model rejection incur a lower loss than an incorrect prediction. Instead, we propose a different distributional perspective, where we seek to find an idealized data distribution which maximizes a pretrained model's performance. This can be formalized via the optimization of a loss's risk with a $ \phi$-divergence regularization term. Through this idealized distribution, a rejection decision can be made by utilizing the density ratio between this distribution and the data distribution. We focus on the setting where our $ \phi $-divergences are specified by the family of $ \alpha $-divergence. Our framework is tested empirically over clean and noisy datasets.
Tempered Calculus for ML: Application to Hyperbolic Model Embedding
Feb 08, 2024



Abstract:Most mathematical distortions used in ML are fundamentally integral in nature: $f$-divergences, Bregman divergences, (regularized) optimal transport distances, integral probability metrics, geodesic distances, etc. In this paper, we unveil a grounded theory and tools which can help improve these distortions to better cope with ML requirements. We start with a generalization of Riemann integration that also encapsulates functions that are not strictly additive but are, more generally, $t$-additive, as in nonextensive statistical mechanics. Notably, this recovers Volterra's product integral as a special case. We then generalize the Fundamental Theorem of calculus using an extension of the (Euclidean) derivative. This, along with a series of more specific Theorems, serves as a basis for results showing how one can specifically design, alter, or change fundamental properties of distortion measures in a simple way, with a special emphasis on geometric- and ML-related properties that are the metricity, hyperbolicity, and encoding. We show how to apply it to a problem that has recently gained traction in ML: hyperbolic embeddings with a "cheap" and accurate encoding along the hyperbolic vs Euclidean scale. We unveil a new application for which the Poincar\'e disk model has very appealing features, and our theory comes in handy: \textit{model} embeddings for boosted combinations of decision trees, trained using the log-loss (trees) and logistic loss (combinations).
Tradeoffs of Diagonal Fisher Information Matrix Estimators
Feb 08, 2024



Abstract:The Fisher information matrix characterizes the local geometry in the parameter space of neural networks. It elucidates insightful theories and useful tools to understand and optimize neural networks. Given its high computational cost, practitioners often use random estimators and evaluate only the diagonal entries. We examine two such estimators, whose accuracy and sample complexity depend on their associated variances. We derive bounds of the variances and instantiate them in regression and classification networks. We navigate trade-offs of both estimators based on analytical and numerical studies. We find that the variance quantities depend on the non-linearity with respect to different parameter groups and should not be neglected when estimating the Fisher information.
Sampled Transformer for Point Sets
Feb 28, 2023Abstract:The sparse transformer can reduce the computational complexity of the self-attention layers to $O(n)$, whilst still being a universal approximator of continuous sequence-to-sequence functions. However, this permutation variant operation is not appropriate for direct application to sets. In this paper, we proposed an $O(n)$ complexity sampled transformer that can process point set elements directly without any additional inductive bias. Our sampled transformer introduces random element sampling, which randomly splits point sets into subsets, followed by applying a shared Hamiltonian self-attention mechanism to each subset. The overall attention mechanism can be viewed as a Hamiltonian cycle in the complete attention graph, and the permutation of point set elements is equivalent to randomly sampling Hamiltonian cycles. This mechanism implements a Monte Carlo simulation of the $O(n^2)$ dense attention connections. We show that it is a universal approximator for continuous set-to-set functions. Experimental results on point-clouds show comparable or better accuracy with significantly reduced computational complexity compared to the dense transformer or alternative sparse attention schemes.
Fair Wrapping for Black-box Predictions
Feb 16, 2022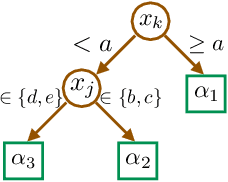
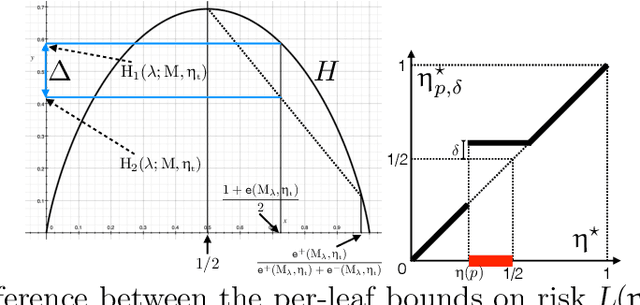
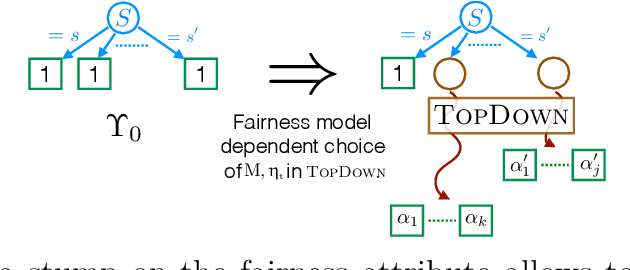
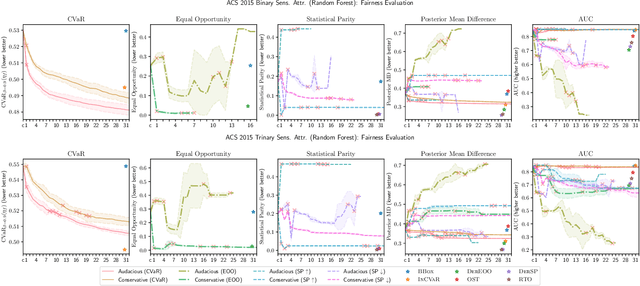
Abstract:We introduce a new family of techniques to post-process ("wrap") a black-box classifier in order to reduce its bias. Our technique builds on the recent analysis of improper loss functions whose optimisation can correct any twist in prediction, unfairness being treated as a twist. In the post-processing, we learn a wrapper function which we define as an {\alpha}-tree, which modifies the prediction. We provide two generic boosting algorithms to learn {\alpha}-trees. We show that our modification has appealing properties in terms of composition of{\alpha}-trees, generalization, interpretability, and KL divergence between modified and original predictions. We exemplify the use of our technique in three fairness notions: conditional value at risk, equality of opportunity, and statistical parity; and provide experiments on several readily available datasets.
Linking Across Data Granularity: Fitting Multivariate Hawkes Processes to Partially Interval-Censored Data
Nov 03, 2021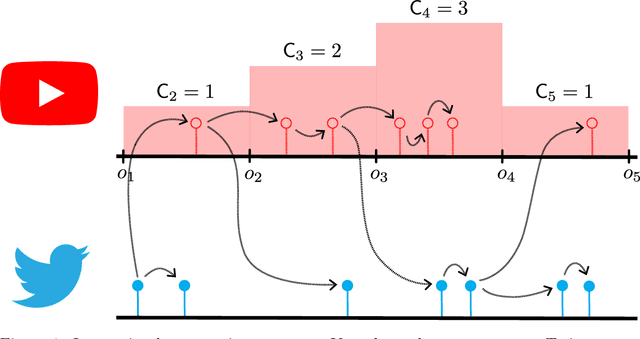
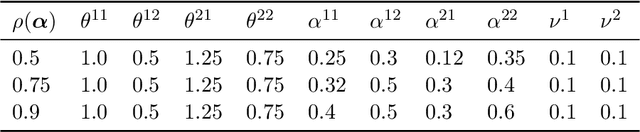
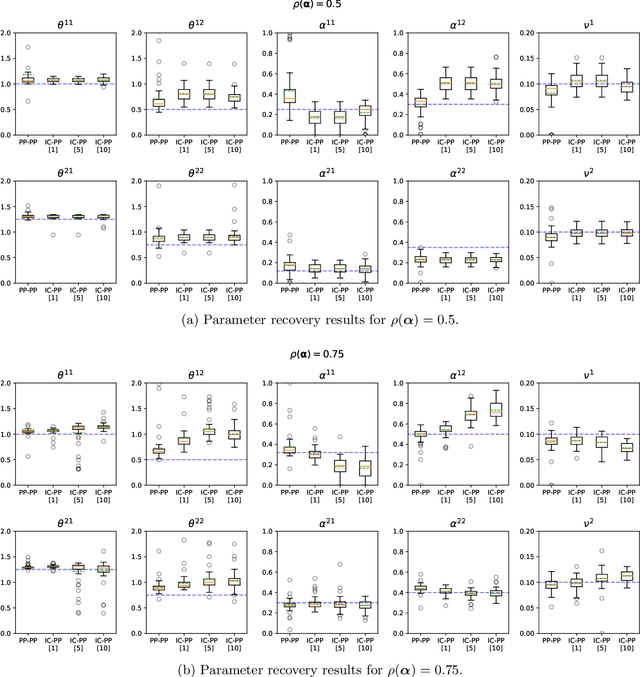
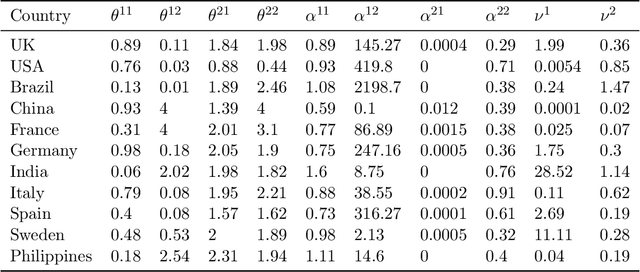
Abstract:This work introduces a novel multivariate temporal point process, the Partial Mean Behavior Poisson (PMBP) process, which can be leveraged to fit the multivariate Hawkes process to partially interval-censored data consisting of a mix of event timestamps on a subset of dimensions and interval-censored event counts on the complementary dimensions. First, we define the PMBP process via its conditional intensity and derive the regularity conditions for subcriticality. We show that both the Hawkes process and the MBP process (Rizoiu et al. (2021)) are special cases of the PMBP process. Second, we provide numerical schemes that enable calculating the conditional intensity and sampling event histories of the PMBP process. Third, we demonstrate the applicability of the PMBP process by empirical testing using synthetic and real-world datasets: We test the capability of the PMBP process to recover multivariate Hawkes parameters given sample event histories of the Hawkes process. Next, we evaluate the PMBP process on the Youtube popularity prediction task and show that it outperforms the current state-of-the-art Hawkes Intensity process (Rizoiu et al. (2017b)). Lastly, on a curated dataset of COVID19 daily case counts and COVID19-related news articles for a sample of countries, we show that clustering on the PMBP-fitted parameters enables a categorization of countries with respect to the country-level interaction of cases and news reporting.
On the Variance of the Fisher Information for Deep Learning
Jul 09, 2021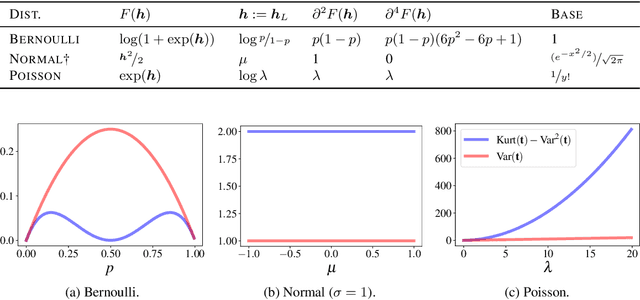
Abstract:The Fisher information matrix (FIM) has been applied to the realm of deep learning. It is closely related to the loss landscape, the variance of the parameters, second order optimization, and deep learning theory. The exact FIM is either unavailable in closed form or too expensive to compute. In practice, it is almost always estimated based on empirical samples. We investigate two such estimators based on two equivalent representations of the FIM. They are both unbiased and consistent with respect to the underlying "true" FIM. Their estimation quality is characterized by their variance given in closed form. We bound their variances and analyze how the parametric structure of a deep neural network can impact the variance. We discuss the meaning of this variance measure and our bounds in the context of deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge